Delaunay Stability via Perturbations
Résumé
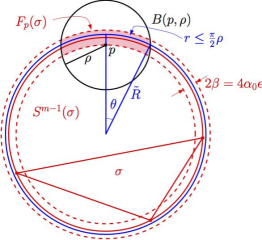
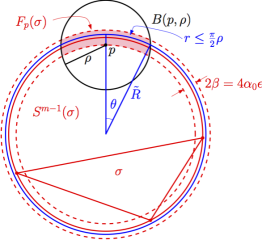
We present an algorithm that takes as input a finite point set in Rm , and performs a perturbation that guarantees that the Delaunay triangulation of the resulting perturbed point set has quantifiable stability with respect to the metric and the point positions. There is also a guarantee on the quality of the simplices: they cannot be too flat. The algorithm provides an alternative tool to the weighting or refinement methods to remove poorly shaped simplices in Delaunay triangulations of arbitrary dimension, but in addition it provides a guarantee of stability for the resulting triangulation.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 flat_pert.pdf (397.95 Ko)
Télécharger le fichier
flat_pert.pdf (397.95 Ko)
Télécharger le fichier
 pert_ball_shell.jpg (47.14 Ko)
Télécharger le fichier
pert_ball_shell.jpg (47.14 Ko)
Télécharger le fichier
 pert_ball_shell.png (95.09 Ko)
Télécharger le fichier
pert_ball_shell.png (95.09 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Origine : Fichiers produits par l'(les) auteur(s)
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Origine : Fichiers produits par l'(les) auteur(s)
Origine : Fichiers produits par l'(les) auteur(s)
Loading...


