Delaunay triangulations of generalized Bolza surfaces
Résumé
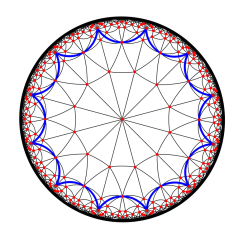
The Bolza surface can be seen as the quotient of the hyperbolic plane, represented by the Poincaré disk model, under the action of the group generated by the hyperbolic isometries identifying opposite sides of a regular octagon centered at the origin. We consider _generalized_ Bolza surfaces Mg, where the octagon is replaced by a regular 4g-gon, leading to a genus g surface.
We propose an extension of Bowyer's algorithm to these surfaces. In particular, we compute the value of the systole of Mg. We also propose algorithms computing small sets of points on Mg that are used to initialize Bowyer's algorithm.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 generalized_Bolza.pdf (6.47 Mo)
Télécharger le fichier
generalized_Bolza.pdf (6.47 Mo)
Télécharger le fichier
 medium.png (50.32 Ko)
Télécharger le fichier
medium.png (50.32 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image


